[알고리즘][자료구조] Tree (트리)

2번째 주제 트리입니다.

 

Tree

그래프의 일종으로 Node가 계층 관계로 1:n 관계를 가지는 자료구조

기본 Tree에서는 용어 정리 정도만.

노드: 각 원소

엣지: Node를 연결하는 선, 부모 노드와 자식 노드를 연결한다.

레벨: 루트에서 노드에 이르는 엣지의 값 (루트는 0)

높이: 노드의 레벨 중 가장 큰 값

루트 노드: 시작원소

형제 노드: 같은 부모를 가지는 Node들

조상 노드: 루트까지의 경로에 있는 모든 노드들

서브 트리: 부모 노드와의 엣지를 끊었을 떄 생기는 트리

자손 노드: 서브 트리에 있는 하위 레벨의 노드들

단말(leaf) 노드: 자식 노드가 없는 노드

노드의 차수(degree): 자식 노드의 개수

 

 

Binary Tree

모든 노드가 자식 트리를 최대 2개까지만 가질 수 있는 트리입니다.

Full Binary Tree(포화 이진 트리): 레벨이 H일 때 가질 수 있는 최대의 개수만큼 Node가 있는 Binary Tree

Complete Binary Tree(완전 이진 트리): 마지막 노드까지 빈 자리가 없는 Binary Tree
(예를 들어 5번이 없으면 탈락이다)

Binary Tree는 Array과 Linked List 형식으로 표현할 수 있습니다.

Array를 사용한다면 루트가 1로 시작할 때, 자식 Index = (부모 Index)*2, (부모 Index)*2 + 1이므로 바로 접근이 가능합니다.

하지만 메모리 공간이 낭비되고 자식 노드가 최대 2개여야 하는 단점.

Linked List를 활용하면 아래처럼 손쉽게 구현이 가능합니다.

class Node {

Data data;

Node left;

Node right;
}

 

 

 

 

 

순회(Traversal)란 각 노드를 중복되지 않게 전부 방문하는 것.

Tree는 비선형 구조이기 때문에 이 선후관계가 없다. 따라서 순회 방법을 정해야 하는데

이러한 이진 트리 구조로 만듦으로써 트리의 원소들에 순회(traversal)하는 것의 기본적인 방법들을 편하게 정의할 수 있게 됩니다..

1.     전위 순회(Preorder traversal): V -> L -> R

2.     중위 순회(Inorder traversal): L -> V -> R

3.     후위 순회(Postorder traversal): L -> R -> V

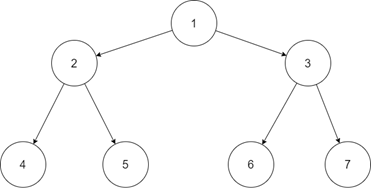
이 그래프를 예로 들면 방문 순서

전위: 1 2 4 5 3 6 7

중위: 4 2 5 1 6 3 7

후위: 4 5 2 6 7 3 1

위처럼 쉽게 구현이 가능해집니다.

 

Binary Search Tree

원소를 추가 될 때 부모 노드보다 크면 L로 아니면 R로 보냅니다.

특정 값을 탐색 시에 log(n)으로 탐색이 가능합니다…

하지만 보통 그냥 Array로 이진탐색을 수행하는게 빠르고 좋습니다.

왜냐하면 Binary Search Tree는 최악의 경우 O(n) 입니다.

(100, 99, 98 ,… 1의 순서로 데이터가 들어오는 경우)

AVL Tree, Red-Black Tree 등 binary search tree의 단점을 해결하기위해 나온 것들도 있지만.. 프로수준에서는 안 나오지 않을까 합니다.

Heap (Priority Queue를 구현한다고 하면 보통 Heap을 의미합니다.

Linked List에서 살펴본 것처럼

추가/삭제/탐색이 O(logn)에 가능합니다.

 

 

 

Heap (Priority Queue)

우선순위가 가장 높은 node를 찾기 위한 자료구조. (Complete Binary Tree)

Linked List와 Array로 만들 수 있지만 일반적으론 Array로 만드는 경우가 많은 거 같아요.

왜냐하면 최대 값이 정해져있기 때문에 메모리에 대한 이득이 없고,
추가 삭제 시에 전체 노드가 바뀌는 것이 아니고 특정 자리만 바뀌기 때문입니다.

 

Max Heap: 높은 값이 우선순위가 높은 것, Min Heap: 낮은 값이 우선 순위가 높은 것.

 

V가 L, R보다 우선순위가 높은 노드로 구성,

단 L과 R 의 관계는 상관없다. (중복 값도 허용합니다)

 

 

삽입 과정:

1.     마지막 노드 다음 비어있는 자리에 새 노드 삽입.

2.     부모 노드와 비교해가면서 부모 노드보다 우선 순위가 높을 시에 자리 교체

3.     루트 노드까지 가면서 2번 반복

 

 

삭제 과정 (혹은 Pop)

1.     루트 노드의 원소 삭제

2.     마지막 노드(타겟 노드)를 루트 노드 자리로 옮기기

3.     타겟 노드를 다음 레벨과 비교하여 다음 레벨의 우선 순위가 더 높으면 자식 노드 중 더 높은 우선순위를 가지는 노드와 자리 교체

4.     리프 노드 까지 진행