TF-IDF
정보 검색과 텍스트 마이닝 등에서 사용되는 가중치이다.
여러 문서로 이루어진 문서군에서 특정 문서 내에서 어느 단어가 얼마나 중요한지를 나타내는 통계적 수치이다.

TF: Term Frequency
하나의 문서 내에 여러 번 등장하는 단어의 중요도는 어떨까?
예를 들면 ChatGPT를 설명하는 글에서는 "ChatGPT" 라는 단어가 아주 잦은 빈도로 등장할 것이다.
이것은 굉장히 중요한 단어이다.
IDF: Inverse Document Frequency
많은 문서에서 등장하는 단어는 어떨까?
예를 들면 "굉장히", "다양한" 같은 단어는 아주 많은 비율의 문서에 적혀있을 것이다.
이것은 중요하지 않은 단어이다.
TF-IDF는 이에 착안하여 특정 단어의 중요도를 나타내는 계산 방식이다.
다만 문서의 숫자가 너무 많아질수록 기하급수적으로 값이 커지니 log를 취한다.
만약 TF-IDF를 이용해서 검색을 한다고 하면
최종적으로 나오는 Token마다 가중치가 나올 것이고 이것의 합이 랭킹 산정에 이용될 것이다.
예를 들면,
" ChatGPT의 역사" 를 검색했다면 "ChatGPT", "역사"로 Tokenizing이 될 것이고
각각의 TF-IDF의 값이 합쳐진 것이 랭킹에 반영될 것이고,
"ChatGPT"가 매칭된 문서는 비교적 큰 랭킹을 가질 것이고
"역사"가 매칭된 문서는 비교적 작은 랭킹을 가지게 될 것이다.
※ "역사"라는 단어가 더 많은 문서에 나오는 것으로 가정한다.
BM25
TF-IDF의 단점은 무엇일까?
1. TF의 선형적 중요도
"ChatGPT"라는 단어가 100번 등장하는 문서는 10번 등장하는 문서보다 10배 중요할까?
이렇게 지나치게 단순한 방식은 좋지 않을 것이라고 직관적으로 알 수 있다.
2. 문서 길이
문서의 길이가 길어지면 TF가 높아지는 것이 일반적일 것이다.
그렇지만 그것이 그 단어의 중요도가 더 높아짐을 의미하지는 않는다.
3. 튜닝
자신의 상황에 맞게 Parameter를 조정하지 못하고 획일된 값을 사용해야 한다.
이를 극복하기 위해 나온 알고리즘이 바로 BM25 이다!!
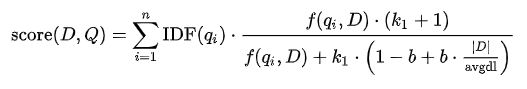
이 BM25를 분석해보자. 크게 2부분으로 나눌 수 있다.
1. IDF 부분
BM25에서는 IDF를 다음과 같이 정의한다.

N: 전체 문서 수
n(qi): 용어 q가 등장하는 전체 문서 수
2. TF 부분

f(qi, D): 특정 문서에서 해당 단어가 나오는 횟수 = TF
k1: parameter
b: parameter
avgdl: 평균 문서 길이
D: 해당 문서 길이
3. Parameter
k는 용어 빈도의 중요도를 결정하는 상수.
b값이 0이라고 생각하고 값을 확인해보자. (내림)
| 빈도 | 0 | 1 | 2 | 10 | 100 | 1000 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 10 | 1 | 1.818 | 2.5 | 5.5 | 9.1818 | 9.9108 |
| 1000 | 1 | 1.998 | 2.994 | 10.891 | 91.81818 | 500.5 |
| 10000 | 1 | 1.9998 | 2.9994 | 10.98901 | 100 | 910 |
| 100000000 | 1 | 1.9999 | 2.999 | 10.999 | 100.99 | 1000.989 |
특정 단어가 여러 번 등장한다고 해서 계속 중요도가 증가하지 않도록 조정된다.
확인할 수 있다시피 k값이 클수록 단어 빈도가 중요하게 반영된다.
따라서 이 k값은 TF의 선형적 중요도을 해소해준다.
일반적으로 1.2 ~ 2 중 사용하며 Elasticsearch에서의 기본값은 1.2이다.
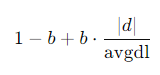
b값을 보자.
위와 같은 값이 분모에 들어가있다.
b가 0이라면 문서의 길이를 고려하지 않는다.
b값이 커질수록 평균 문서 길이 대비 해당 문서의 길이가 더 크게 반영된다.
이면 문서 길이가 길어질수록 해당 값이 커지고,
해당 TF의 가중치는 낮아진다. (분모에 있으므로!)
그리고 b가 커질 수록 반영되는 문서 길이가 반영되는 비율은 더 커진다!
따라서 이 b값은 TF-IDF의 단점인 문서 길이를 해소해 준다.
일반적으로 0.75 값을 사용하며 Elasticsearch에서 이 값을 기본값으로 사용한다.
이러한 장점 때문에 Elasticsearch는 BM25를 기본 검색랭킹 알고리즘으로 사용하고 있다.
물론 상황에 맞게 랭킹 알고리즘을 산정하는 것 또한 매우 중요하다.
예를 들면, Exact Match 된 경우 무조건 Ranking 1등이라든가.
'Elasticsearch (엘라스틱서치)' 카테고리의 다른 글
| Elasticsearch (엘라스틱서치)의 Indexing 파일 - Segment (0) | 2022.09.13 |
|---|---|
| Elasticsearch (엘라스틱서치)의 Indexing 방식 - Inverted Index (0) | 2022.09.02 |
| Elasticsearch (엘라스틱서치)의 Search Process (0) | 2022.09.02 |
| Elasticsearch (엘라스틱서치)의 Indexing Process (0) | 2022.09.02 |
| Elasticsearch (엘라스틱서치) vm.max_map_count 버그 해결 (0) | 2021.04.10 |